ChromSword Offline
Experience your peaks elution time by building computer-assisted simulations.
What is computer-assisted simulation?
Possibility to simulate chromatographic conditions based on the existing chromatographic or structural data.
What kind of data can be used?
- Use experimental data from your chromatographic experiments
- Use structural formulae and column characteristics
What method variables can be simulated out of the chromatographic data?
- Gradient profile (including different isocratic conditions)
- pH influence on the separation
- Temperature effect
- Combination of several parameters mentioned above
Data input is simple
- Choose the data to input
- Use the data
- Select the optimization model
Optimize gradient
ChromSword has the unique linear and milti-step optimization of gradient methods using a super-fast Monte-Carlo method.
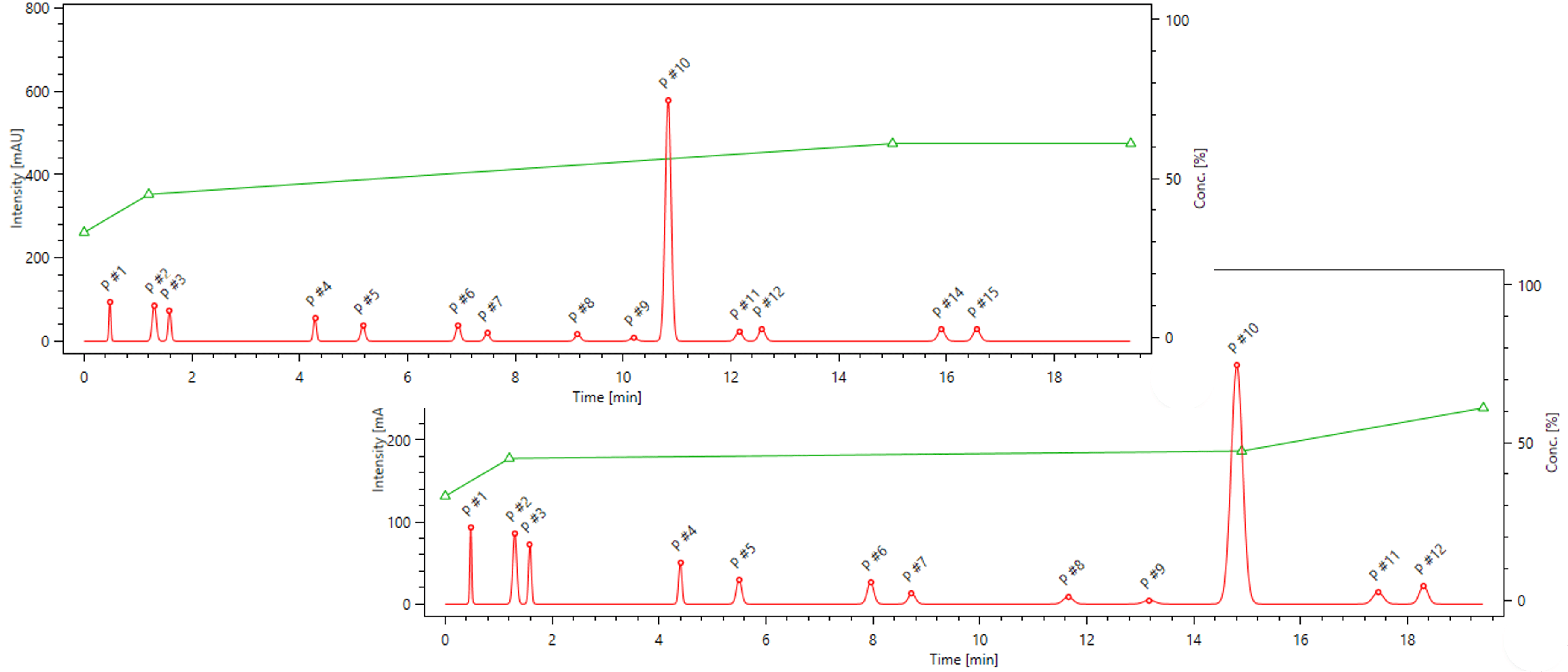
Optimizing temperatures
By analyzing the retention data, ChromSword determines, and then refines the parameters of the retention model elution for the column being used; and predicts the conditions for the best separation. If you use the model with the power one, ChromSword also determines the enthalpy of sorption from the retention model:
ln k = ln k + H / (RT) 0 D
where H is the enthalpy of sorption of a solute in kJ/mol.
R is the gas constant.

Procedure for optimizing pH in reversed-phase HPLC
When your sample contains basic or acidic compounds with ionizable atoms or groups, pH is a very effective tool for optimizing the separation. ChromSword supports two mathematical procedures for optimizing pH in reversed-phase HPLC. The first procedure is based on applying polynomials with powers up to 6. The second procedure determines, the nature of solutes (neutral, acidic, basic) their pK value and then builds their retention models by using the retention data obtained with different pH values of a mobile phase.
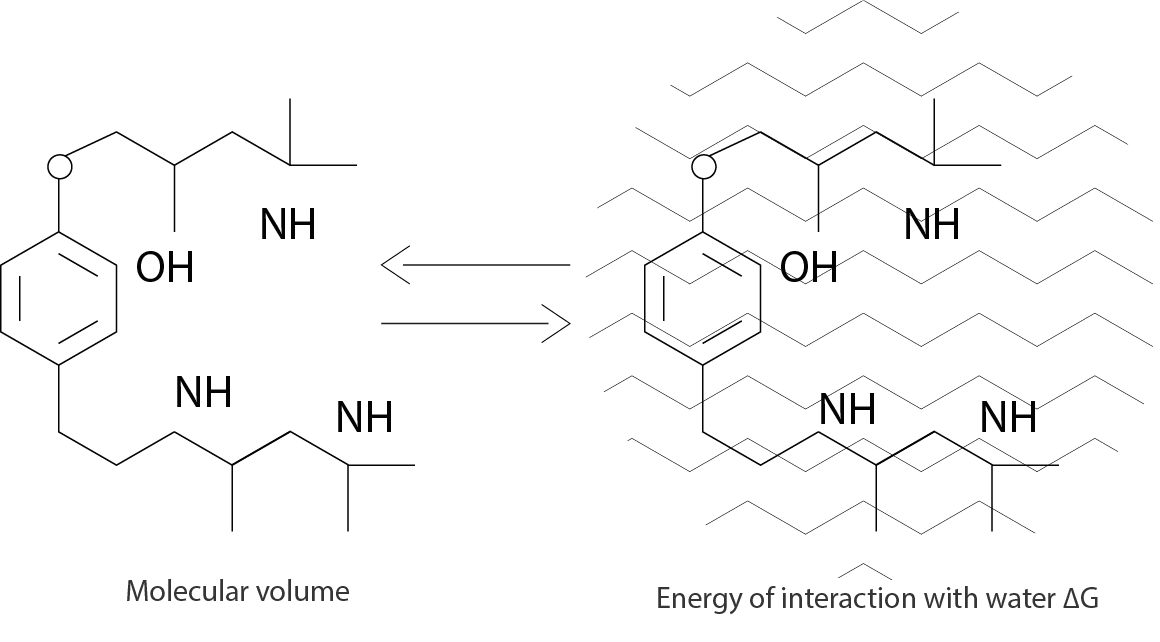
Predictions based only on structural formula
The unique ChromSword approach lets the user to start the simulation without experimental data by inputting structural formulas of analytes and applying the Solvatic retention model:
ln k’ = a V^(2/3) + b ΔG + c
where V is the molecular volume of a solute, ΔG is the energy of interaction of a solute with water, a, b and c are the parameters which are determined by the characteristics of a reversed phase column in the eluent being used.
This is a new concept and ChromSword’s unique software that supports it
With this approach, you work more precisely and rapidly than that based on formal linear and quadratic polynomial models but it requires that both the parameters of the solutes (volume and energy of interaction with water) and the characteristics of the reversed-phase column under experimental conditions be known.
Optimizing two variables simultaneously
Optimization of two variables is an effective tool for improving and development of HPLC methods. ChromSword provides all necessary interface and mathematical procedures for optimization of two chromatographic variables simultaneously. The following two variables can be optimized with ChromSword.
